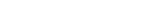Conferencias y seminarios
Identidades de expectación cuánticas y otros tópicos de mecánica estadística
Informaciones
- Mario Riquelme
- marioriquelme@uchile.cl
Fecha
Viernes 11 de octubre de 2024
Hora
16:15
Lugar
Sala F12
(Edificio de Física)Organiza
Charlista: Boris Maulen, UNAB
Resumen: Bajo la formulación Bayesiana de las probabilidades, es posible derivar identidades de expectación que, entre otrasutilidades, permiten obtener de manera indirecta los momentos asociados a una distribución estadística. Estas identidades son, a saber, el teorema de fluctuación-disipación y el teorema de variables conjugadas, los que a su vez, han mostrado supotencialidad en el contexto de mecánica estadística clásica al agrupar diversos teoremas de la física en un esquema unitario, además de permitir la obtención de nuevas identidades en el área. Desde esta perspectiva, diversas identidades deexpectación provenientes de los modelos canónicos y gran-canónico, resultan ser casos particulares del teorema de fluctuación-disipación Bayesiano. Por otro lado, son corolarios del teorema de variables conjugadas las relaciones del virial, el teorema de equipartición de energía y, más importante aún, el estimador de temperatura inversa de Rugh y Rickayzen.
En este trabajo mostramos que es posible, por medio de herramientas matemáticas provenientes de teoría de grupos y álgebras de operadores en espacios de Hilbert, llevar tanto el teorema de fluctuación-disipación como el teorema de variables conjugadas a sus respectivas versiones cuánticas. Exponemos además que, al escoger una matriz de densidad del modelo canónico, resulta posible proponer un estimador de temperatura inversa que, además, es un operador hermítico con espectro continuo. Finalmente, contrastamos las relaciones encontradas para el estimador-operador de temperatura inversa con sus equivalentes clásicos.